Concepts of survival function estimations and corresponding calculations both manually and in R.

Introduction

In the Survival Analysis 1: Basic concepts and three fundamental functions I
shared about the three basic blocks of survival analysis: density function,
survival function and hazard function.

Next, it is natural to think about: now we know their meaning, but how
to estimate them? It brings us to the next topic of non-parametric estimation
of survival functions. The word non-parametric means there is no
assumption about the distribution of survival time T.

A simple case without censoring

No censoring indicates all samples are observed until they experience the event of
interest (e.g., death, unemployment, account deletion). Then we can
estimate survival function S(t) by:

$\hat{S}_{t_{i}} = \frac{\text{number of individuals survived longer than t}}{\text{total number of individuals in the sample}}$

Assume we are observing 8 mice’ survival time

Time	Accumulate death number	$\hat{S}_{t_{i}}$
2	3	$\frac{8-3}{8} = \frac{5}{8} = 0.625$
4	5	$\frac{8-5}{8} = \frac{3}{8} = 0.375$
12	8	$\frac{8-8}{8}$ = 0

Estimation with consoring

The method above is applicable only in situations where all individuals
are observed until the events of interest occur (no censoring). However,
in real life, such a scenario is rare because of unfeasible study
design, high expenses, etc. As a result, we have to adjust the risk
set accordingly when new observations are entering the study or
previous ones are being censored. Two common methods are Life-Table
(Actuarial) and Product-Limit (Kaplan-Meier) methods.

The Life-Table (Actuarial) method

This method objectively defines the time intervals by split points and
assume the observations being censored within an interval were at risk
for half of the length of that interval. Let me first introduce some
jargon:

• The split points = $0 \le \tau_{1} \le \tau_{2} ...\le \tau_{k}$
• Then the time intervals = $I_{r} = [\tau_{r}, \tau_{r+1})$
• The number of observations enter the $r^{th}$ interval = $N_{r}$
• The number of observations experiencing the event in the $r^{th}$
  interval = $E_{r}$
• The number of observations censored in the $r^{th}$ interval = $Z_{r}$
• Therefore we have $N_{r} = N_{r-1} - E_{r-1} - Z_{r-1}$
• The risk set (observations exposed to risk of experiencing the event)
  = $R_{r} = N_{r} - 0.5*Z_{r}$. The “$0.5 * Z_{r}$” part comes from the
  assumption mentioned above.

Next, we can compute conditional probability of experiencing the
event in the $r^{th}$ interval:

$\hat{q}_{r} = \frac{E_{r}}{R_{r}}$

The conditional probability of surviving the $r^{th}$ interval:

$\hat{p}_{r} = 1 - \hat{q}_{r}$

Finally we can compute the survivor function as

• when r = 0:

$\hat{S}_{0} = 1$

• for r = 1, 2, 3, …

$\hat{S}_{r} = \hat{p}_{r-1} * \hat{S}_{r-1} = \hat{p}_{r-1} * (\hat{p}_{r-2} * \hat{S}_{r-2}) = ... = \prod_{i=1}^{r-1}\hat{p}_{i}$

• with standard error estimation

$SE(\hat{S}_{r}) = \sqrt{\hat{S}_{r}^{2} (\sum_{i=1}^{r} \frac{\hat{q}_{i}}{\hat{p}_{i} R_{i}})}$

• density function

$\hat{f}_{r} = \frac{\hat{S}_{r-1} - \hat{S}_{r}}{\tau_{r} - \tau_{r-1}}$

• with standard error estimation

$SE(\hat{f}_{r}) = \sqrt{(\frac{\hat{q}_{r}\hat{S}_{r}}{\tau_{r+1}-\tau_{r}})^{2} (\sum_{i=1}^{r-1} \frac{\hat{q}_{i}}{\hat{p}_{i}R_{i}} + \frac{\hat{p}_{r}}{\hat{q}_{r}R_{r}})}$

• the hazard function is estimated by

$\hat{h}_{r} = \frac{E_{r}}{(R_{r} - \frac{E_{r}}{2}) (\tau_{r+1}-\tau_{r})}$

• with standard error estimation

$SE(\hat{h}_{r}) = \sqrt{\frac{\hat{h}^{2}_{r}}{\hat{q}_{r}R_{r}} [1 - (\frac{\hat{h}(\tau_{r+1} - \tau_{r})}{2})^{2}]}$

A simple exercise

The following table contains data on the recidivism-example in Allison
(2010, p. 45):

interval_start	num_entering	num_withdrawn	num_exposed_risk	num_events
0	432	0	432	14
10	418	0	418	21
20	397	0	397	23
30	374	0	374	23
40	351	0	351	26
50	325	318	166	7

Example data

Based on the values in the table, let’s manually estimate the survival
function, density function, and hazard function together with their
standard errors.

• When r = 0

$\hat{S_{r}} = 1$

• When r = 1

$E_{r}$ = 14, $Z_{r}$ = 0, $N_{r}$ = 432, $R_{r}$ = 432

$\hat{q_{r}} = \frac{E_{r}}{R_{r}} = \frac{14}{432} = 0.03240741$

$\hat{p_{r}} = 1 - \hat{q_{r}} = 1 - \frac{14}{432} = 0.9675926$

$\hat{S_{r}} = \prod_{i = 1}^{r}\hat{p}_{i} = 0.9675926$

$SE(\hat{S_{r}}) = \sqrt{\hat{S_{r}}^{2} (\sum_{i=1}^{r-1} \frac{\hat{q}_{i}}{\hat{p}_{i} R_{i}})} = \sqrt{1^{2} (\frac{0.03240741}{0.9675926 * 432})} = 0.0087$

$\hat{f_{r}} = \frac{\hat{S}_{r-1} - \hat{S}_{r}}{\tau_{r} - \tau_{r-1}} = \frac{1 - 0.9675926}{10} = 0.00324074$

$\begin{aligned} SE(\hat{f_{r}}) & = \sqrt{(\frac{\hat{q_{r}}\hat{S}_{r}}{\tau_{r+1}-\tau_{r}})^{2} (\sum_{i=1}^{r-1} \frac{\hat{q_{i}}}{\hat{p}_{i}R_{i}} + \frac{\hat{p}_{r}}{\hat{q}_{r}R_{r}})} \\ &= \sqrt{(\frac{0.032}{10})^{2}(\frac{0.032}{0.968*432} + \frac{0.968}{0.032*432})} \\ & = 0.000847243 \end{aligned}$

$\hat{h}_{r} = \frac{E_{r}}{(R_{r} - \frac{E_{r}}{2}) (\tau_{r+1}-\tau_{r})} = \frac{14}{(432 - 14/2)10} = 0.003294118$

$\begin{aligned} SE(\hat{h}_{r}) & = \sqrt{\frac{\hat{h}^{2}_{r}}{\hat{q}_{r}R_{r}} [1 - (\frac{\hat{h}_{r}(\tau_{r+1} - \tau_{r})}{2})^{2}]} \\ &= \sqrt{\frac{0.003294118^{2}}{0.03240741 * 432} [1 - (\frac{0.003294118* 10}{2})^{2}]} \\ & = 0.0008802706 \end{aligned}$

• For r > 2, I will calculate them with R.

# input data
tau_interval <- 10
r <- 1:6
i <- seq(0, 50, 10)
Nr <- c(432, 418, 397, 374, 351, 325)
Zr <- c(0, 0, 0, 0, 0, 318)
Rr <- c(432, 418, 397, 374, 351, 166)
Er <- c(14, 21, 23, 23, 26, 7)

# by definition
qr <- Er / Rr
pr <- 1 - qr
hr <- Er / ((Rr - Er / 2) * tau_interval)
Sr <- c()
Sr[1] <- pr[1]
for (i in 2:6) {
  Sr[i] <- Sr[i - 1] * pr[i]
}

fr <- c()
fr[1] <- 1 - Sr[1]

for (i in 2:6) {
  fr[i] <- (Sr[i - 1] - Sr[i]) / tau_interval
}


# find se

se_sr <- c()
inner_sum <- qr[1] / (pr[1] * Rr[1])
se_sr[1] <- sqrt(Sr[1]^2 * inner_sum)
for (i in 2:6) {
  inner_sum <- inner_sum + qr[i] / (pr[i] * Rr[i])
  se_sr[i] <- sqrt(Sr[i]^2 * inner_sum)
}

se_fr <- c()
inner_sum <- qr[1] / (pr[1] * Rr[1])
se_fr[1] <- sqrt(((qr[1] * Sr[1] / tau_interval)^2) * (inner_sum + pr[1] / (qr[1] * Rr[1])))
# se_fr[1] = sqrt(((qr[1] * Sr[1]/ tau_interval)^2) * (1 + pr[1]/(qr[1] * Rr[1])))
for (i in 2:6) {
  inner_sum <- inner_sum + qr[i] / (pr[i] * Rr[i])
  se_fr[i] <- sqrt((qr[i] * Sr[i] / tau_interval)^2 * (inner_sum + pr[i] / (qr[i] * Rr[i])))
}

se_hr <- c()
for (i in 1:6) {
  se_hr[i] <- sqrt((hr[i]^2 / (qr[i] * Rr[i])) * (1 - (hr[i] * tau_interval) / 2)^2)
}

df1 <- tibble::tibble(r, i, Nr, Zr, Rr, Er, qr, pr)
df2 <- tibble::tibble(Sr, se_sr, fr, se_fr, hr, se_hr)

r	i	Nr	Zr	Rr	Er	qr	pr
1	6	432	0	432	14	0.032	0.968
2	6	418	0	418	21	0.050	0.950
3	6	397	0	397	23	0.058	0.942
4	6	374	0	374	23	0.061	0.939
5	6	351	0	351	26	0.074	0.926
6	6	325	318	166	7	0.042	0.958

Example data

Sr	se_sr	fr	se_fr	hr	se_hr
0.968	0.009	0.032	0.001	0.003	0.001
0.919	0.013	0.005	0.001	0.005	0.001
0.866	0.016	0.005	0.001	0.006	0.001
0.812	0.019	0.005	0.001	0.006	0.001
0.752	0.021	0.006	0.001	0.008	0.001
0.721	0.023	0.003	0.001	0.004	0.002

Derived functions and corresponding standard error

The Kaplan-Meier (Product-Limit) Method

One helpful YouTube video to cover this method is from “zedstatistics”
here.

Its estimation is similar to life-table method above:

$\hat{S}(t) = \prod_{r:\tau_{r}\le t}(1 - \frac{E_{r}}{R_{r}})$

$V(ln(S(t))) = \sum_{t(i)\le t}\frac{E_{r}}{R_{r}(R_{r} - E_{r})}$

I really enjoy the fact that YouTube video step by step deducts the
stand error
$V(ln(S(t))) = \sum_{t(i)\le t}\frac{E_{r}}{R_{r}(R_{r} - E_{r})}$.
Please check it out if interested!

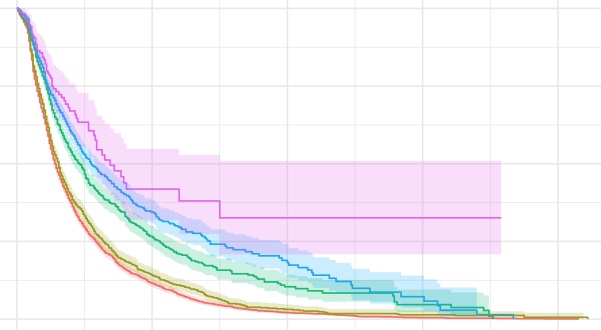
If you plot out the survival function versus the time, then you can get
the survival curve, which is often used in the observational data
analysis.

A simple exercise

The example data is from the survival analysis course at SU.

• To estimate the survival curves (Kaplan-Meier method), we need to use
  survival library in R.

library(survival)
library(tidyverse)

• Create a survival object with Surv() function.

# read data
df <- readxl::read_excel("nonparametric_estimation/data/example_data.xlsx")
# create a survival object
birth_time <- Surv(df$ExpMonths, df$FirstBirth)

• Kaplan-Meier estimation for the different levels of birth cohort

km_BirCoh <- survfit(birth_time ~ as.factor(BirCoh), data = df)

• Plot the curve

plot(km_BirCoh, main = "Survival curve: Kaplan-Meier estimates")

• or we can have a better looking curve by using survfit2 from
  ggsurvfit package.

library(ggsurvfit)
survfit2(birth_time ~ as.factor(BirCoh), data = df) %>%
  ggsurvfit() +
  labs(
    x = "Months",
    y = "Survival probability",
    title = "Survival curve: Kaplan-Meier estimates",
    color = "Birth cohort"
  ) +
  theme(plot.title = element_text(hjust = 0.5)) +
  add_confidence_interval()

Please note: since the confidence intervals are symmetric, when the
estimated survivor function is close to 0 or 1, they may sit outside the
(0,1) range. One solution is to manually enclose interval with 0 or 1.
This is also mentioned in the video above.

• The cumulative hazard function H(t) is estimated by

$\hat{H}(t) = - log[\hat{S}(t)]$

If we plot H(t) versus the time t, finding the slope is constant, then
it indicates that the hazard rate is constant over time.

Life-table VS Kaplan-Meier

1. Life-table uses aggregated data, with arbitrary choice of interval.
   This may lead to loss of information; Kaplan-Meier does not demand
   grouping of data. It records every spot when event of interest
   happens. Therefore we can get more information from Kaplan-Meier.
2. However, one shortcoming of Kaplan-Meier is that if one prints out
   the estimations, it could be a very long table.

End thoughts

The derivation of life-table and Kaplan-Meier methods to estimate the
survival functions are intuitive and straightforward. It does not involve
complicated algebraic calculations. I feel the “statistical spices”
comes from the confidence interval and standard error estimation, which
are based on the theory of sampling distribution of the mean.

So now we know how to estimate the functions. In the next post, we will look at the comparison of two survival functions.